Desktop Applications

I wrote these applications in C++11 with the wxWidgets GUI engine. This page is primarily intended for people who would like some high-level background on the applications themselves.

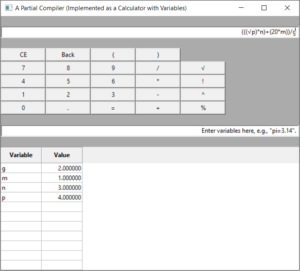
A Partial Compiler

First, the theory. This is one implementation of a context-free language, namely, a type 2 (context-free) grammar in the Chomsky Hierarchy, with a recognizing machine in the form of a recursive descent LL(1) pushdown automaton (PDA).

Theoretical Details: Languages, Grammars, and Machines (Automata)

For an explanation of all this, a couple of definitions are in order before getting into this application's implementation.

Formal Language. A (possibly infinite) set of strings created from an alphabet of terminal symbols.
- Alphabet. A finite set of symbols used to create the strings of a formal language.
  - Alphabets come in two sets:
    - Terminals. Symbols actually present in the final string. The set of terminals is conventionally denoted with the Greek capital sigma ('S' in our script for 'Symbol set'), '$\Sigma$'.
    - Non-terminals. Symbols that are used in production rules until all that is left are terminals. Non-terminals are usually denoted by the set $N$. Non-terminals are conventionally given as capital letters, whereas terminal strings are in lower-case.
Formal Grammar. A set of production rules; namely, the rules which can be used with an alphabet $N \cup \Sigma$ to recognize a formal language.
- Production Rules (aka Rules, aka Rewrite Rules). Just what they sound like: a production rule takes a symbol, and can re-write it as another symbol or string of symbols. For example, $$A \Longrightarrow aA$$
  - In this example, we have taken the non-terminal $A$, and re-written it as $aA$.
  - The '$\Longrightarrow$' means 'implication', just as in the rest of logic and mathematics: you can convert $A$ into $aA$, but you cannot convert the other way around by the axioms of this grammar.
Machines/Automata. Machines recognize if a particular string is a part of the formal language, or not, through the production rules of the formal language's formal grammar.

Context-Free Grammars

Linguistic context is the linguistic environment which surrounds the occurrence of a particular constituent. A constituent is a terminal or non-terminal symbol; more basically, anything from the alphabet of this particular language.

- For example, a constituent $\beta$ occurs in some linguistic environment, some syntactic context: $$\_\_ \beta \_\_$$
- Assume the two '__' of context were filled in: '$\alpha\beta\gamma$'. This would mean that the syntactic constituent '$\beta$' can only occur between the two other constituents '$\alpha$' and '$\gamma$'. If either or both of them are missing, '$\beta$' will not be recognized by the machine (i.e., it will be ungrammatical).

Linguistic context was used as far back as 1942 by the structural linguist Zellig Harris (Morpheme alternants in linguistic analysis. Language, 18:169-180. 1942). Harris was Chomsky's teacher and an enormous influence on generative grammar.

A 'context-free' grammar refers to anything on the left hand side of the production (i.e., everything to the left of the arrow, e.g., $A \Longrightarrow \ldots$) having no context, namely: there can be no letters whatsoever around the non-terminal $A$ on the left-hand side of the arrow. If there are, then they are the context of that non-terminal, and we no longer have a context-free grammar.

An LL(1) Recursive Descent Parser

The First 'L':Left-to-right reading of input. So the string '(a + b)' would be read ?rst as the character '(', then 'a', then '+' (spaces are ignored), then 'b', and ?nally ' )'.
The Second 'L': A Leftmost derivation. Namely, on the right hand side of productions, we derive the leftmost non-terminal of the string. For example, in $$S \Longrightarrow AB$$
- The $A$ is substituted first, then the $B$ is substituted on another iteration, after $A$.
The (1): We look ahead by 1 character, and that is enough to determine the next course of action.

Recursive Descent Parser. A top-down (descending), recursive parser, in this case LL(1). The parser can be thought of as creating a (graph-theoretic) abstract syntax tree. Then it starts from the left of the string and moves to the right character-by-character, with the next character being put into the lookahead to determine the next course of action.

There you have the theory, where everything is in the abstract. You can do it on paper, but there is no real-world, 1-to-1 equivalent (for example, no program) to the abstractions you play with on paper.

Here's an actual program that puts this into practice. Quickly we find that we have to attend to many other factors besides a cleaned-up abstraction that the theory provides.

Putting It into Practice: Our Limited Compiler

The compiler is only partial because it has all of the analytical parts of a compiler: a lexical analyzer, a syntactic analyzer with semantic analysis, and both a symbol table and error handler (which both operate throughout the entire program, including translation, i.e., code generation). However, it does not do any translation into a lower-level language like assembly language or machine language. Instead, it gives the output of a standard calculator.

The partial compiler is where theory meets practice; where the rubber meets the messy road. As always in any science, practice is necessarily more disorderly than the clean abstraction of theory.

Here, then, is what the program actually consists of.

Lexical Analyzer: Tokens

The lexical analyzer takes any input whatever, and distills from it only numbers/characters without spaces, as much as possible. If any of these strings is not an enduser-defined variable, the GUI will tell the user to input only valid formulas.

Strings are a concatenation of characters. We look at each character individually. If the character is a letter instead of a number, operator, or parenthesis, the program first looks at all letters starting from that first one, all the way up until the next number, operator, or parenthesis. Then it checks the string of letters against the symbol-table to see if it matches any of our user-defined variables.

Syntax Analyzer: An LL(1) Recursive Descent Parser

We have implemented the abstract grammar into a concrete recursive descent parser. This includes semantic analysis: if our operator is addition, we define what the machine does (the semantics) very differently from e.g., multiplication.

The recursion is indirect: function A calls function B calls function C calls function A.

A Quick Run Through the Program

The program gets the first token: a number, an open parenthesis, or a previously user-defined variable. If none of these are present, the program will tell you. It then runs the lookahead function on this token, putting it in the buffer, so it can use this token as its LL(1) lookahead token. This is before the rest of the syntax analyzer functions are run, so that it will truly be a look ahead.

Next, the program dives into syntax analysis proper. Here there is a (recursive) chain of functions. These functions, i.e., C++'s internal stack, plays the role of the pushdown automaton. Because it is Last In, First Out (LIFO) order, we get operator precedence as a reverse of the functions called first. Namely, the last function to be called (recursively) is effectively the first function to be executed. This is how we determine order of operations: unless there are parentheses, the order is as follows: the last function to be called, gets the result back first.

A screenshot of this program follows (click to enlarge in a separate tab):

The Truth Table Application

This app is to help you out with your studies of formal logic. Enter the formula, and it will return a truth-table with all the subformulas showing their values as well.

The truth-table application:

Takes input from the user.
Standardizes the parentheses from that input with Dijkstra's Shunting-Yard Algorithm. This includes cases where the user did not put in parentheses at all. To resolve this, our program's precedence rules are as follows:
- From left to right, '¬' comes before before '?' in creating the parentheses; then '?' before '?' before '?' before '?'.
- The shunting-yard algorithm removes all parentheses, because they become redundant. It puts the entered formula into postfix notation (i.e., reverse Polish notation, RPN). This causes the formula to become functional; namely, once in RPN the formula is readable by the compiler in 1 and only 1 way. You need parentheses and/or precedence rules to convert from infix notation to reverse Polish notation, but not the other way around.
Next, the program provides each letter with all truth-values possible: where n is the number of sentence letters in the formula, we get 2ⁿ truth value rows in all.
Finally, the program re-converts from postfix notation into infix notation.
- Here, we can control exactly where/how to place the parentheses in moving from a functional postfix notation, to an infix notation which has by definition more than one way of interpreting a 3+ operand expression.
  - For example, the formula without parentheses 'A?B?C' could be interpreted as '((A?B)?C)' or '(A?(B?C))', giving very different results.
- We make sure all binary operators are left-associative. This matches C++'s operator associativity of its logical operators, and results in a functional output of postfix-to-infix notation.

Here is a screenshot of the application (click to enlarge in a separate tab):

Why C++?

I used C++11 for coding both of these applications, because C++ gives as much (or nearly as much) control over the machine's memory as is possible for a high-level language.

C++ also has many faults, though they're still around mostly because of backwards-compatibility. For example, we wouldn't want the C++ code on the Mars rovers to become obsolete any time soon.

And there's always a trade-off: control for ease of programming.

For example, C++ has the option of either putting a class object on the stack or on the heap. The default is to place it on the stack. But if you put an object on the heap with the new keyword, you must delete it to avoid memory leaks. It can be very difficult to remember to do this at all times, especially for longer/more complex applications that give your human memory a good workout.

"Resource Acquisition Is Initialization" (RAII) is a technique which puts all new keywords in a class's constructor, all deletes in its destructor, and so is a solution to this problem of human memory, focus, and attention. But you still have to remember to use RAII in your designs, and it takes quite a few more lines of code to do it right. This is just one example of the near absolute control C++ provides, at the trade-off of having to be explicit in your memory allocation code.

Java on the other hand has no equivalent to this. Java only gives you the option of creating an object with the new operator: there are no class objects on the stack. Then Java deletes the objects with its garbage collector whenever it deems appropriate: there's nothing you can do to delete the objects yourself. Though this trade-off eliminates a large aspect of human error, it also removes very much control over how your program does what it does. It's all a balance of what you really need.

C++ also gives you the ability to explicitly pass, return, and move objects in the following ways:

By value. Pass/return a copy of the object (i.e., the built-in or user-defined type).
By reference. Really a pointer under the hood that doesn't allow for many of the mistakes people often make with pointers.
By pointer. Passes a pointer variable (4 bytes on this machine) to a function. The pointer points to an object. Dereference this pointer and you get, through indirection, the object itself, without having passed this object. Lots of gotchas here; it's much better/more convenient to pass by reference whenever possible.
Move. Create a shallow copy of the object — a second pointer to the object itself — then erase the old pointer.

In short, other languages simplify the developer's life by removing various degrees of control of the machine. So long as the language is (semantically) Turing complete, there are certain times when this is better. For example, for any web applications, Node or PHP are (much) more direct than C++. But C++ is still king of control, and because I created these two applications as desktop applications, I wanted full control of how I went about programming them.